Question 1 (a): Consider the language S*, where S = {aa, b). How many words does this language have of length 4? of length 5? of length 6? What can be said in general?
The language S* is the Kleene closure of S, which means it contains all possible strings that can be formed by concatenating zero or more strings from S. In this case, S = {aa, b}, so S* contains all strings that can be formed by concatenating zero or more instances of “aa” and “b”.
Let’s denote the number of words of length n as W(n).
- For length 4, the possibilities are “aaaa”, “aabb”, “bbaa”, “bbbb”, so W(4) = 4.
- For length 5, there are no words because neither “aa” nor “b” can form a string of length 5, so W(5) = 0.
- For length 6, the possibilities are “aaaaaa”, “aaaabb”, “bbaaaa”, “aabbaa”, “bbaabb”, “bbaaab”, “abbaaa”, “bbbbbb”, so W(6) = 8.
In general, for a given length n:
- If n is odd, there are no words of that length, so W(n) = 0.
- If n is even, the number of words is 2^(n/2), because each position can be filled by either “aa” or “b”.
So, the function W(n) can be defined as follows:
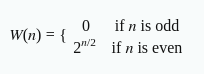
This is because each pair of positions can be filled independently with either “aa” or “b”, and there are n/2 such pairs in a string of length n. Therefore, there are 2^(n/2) different ways to fill these positions. If n is odd, it’s not possible to fill all positions with “aa” or “b”, so there are no words of that length.
Question 1 (b): Let S = {ab, bb; and let T = {ab, bb, bbbb}. Show that S* = T*
The Kleene closure S* of a set S is the set of all strings that can be formed by concatenating zero or more strings from S. In this case, S = {ab, bb} and T = {ab, bb, bbbb}.
Let’s see if S* equals T*:
- Every string in S* is certainly in T* because every string in S is in T.
- Now, consider a string in T*. If it’s in S, we’re done. If it’s not in S, then it must be “bbbb”. But “bbbb” can be formed by concatenating two “bb”s, and “bb” is in S. Therefore, “bbbb” is in S*.
So every string in T* is also in S*.
Therefore, we can conclude that S* = T*. This shows that even though S and T are different, their Kleene closures are the same because you can form the same set of strings by concatenating strings from S or T. This is a nice example of how different sets can have the same Kleene closure. It’s also a reminder that when working with Kleene closures, it’s important to consider not just the strings in the set, but also the strings that can be formed by concatenating those strings.
Congratulations on completing two free questions! To continue your quest for knowledge and unlock the full solution of TOC PYQ 2017 Solution, consider purchasing our full solution by clicking here.
We also have an exclusive discount on the 2017 + 2019 solution Bundle for you, if you want to purchase both solution once then you can click here to purchase the bundle to get ₹100 off.
